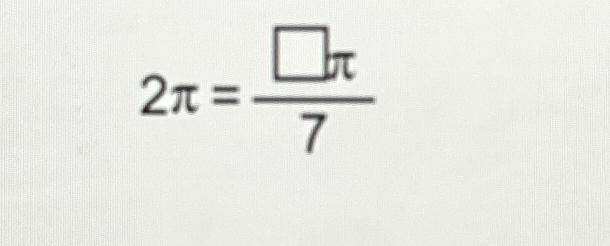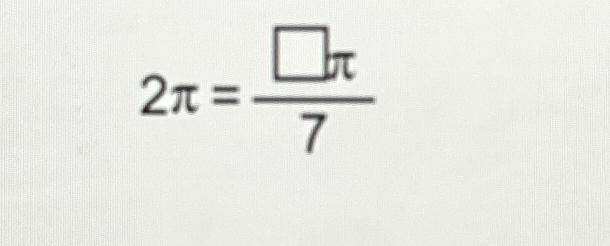Proof that 22/7 exceeds π

Proofs of the mathematical result that the rational number ⁠22/7⁠ is greater than π (pi) date back to antiquity. One of these proofs, more recently developed but requiring only elementary techniques from calculus, has attracted attention in modern mathematics due to its mathematical elegance and its connections to the theory of Diophantine approximations. Stephen Lucas calls this proof "one of the more beautiful results related to approximating π". Julian Havil ends a discussion of continued fraction approximations of π with the result, describing it as "impossible to resist mentioning" in that context.

The purpose of the proof is not primarily to convince its readers that ⁠22/7⁠ (or ⁠3 1/7⁠) is indeed bigger than π. Systematic methods of computing the value of π exist. If one knows that π is approximately 3.14159, then it trivially follows that π < ⁠22/7⁠, which is approximately 3.142857. But it takes much less work to show that π < ⁠22/7⁠ by the method used in this proof than to show that π is approximately 3.14159.

Background

⁠22/7⁠ is a widely used Diophantine approximation of π. It is a convergent in the simple continued fraction expansion of π. It is greater than π, as can be readily seen in the decimal expansions of these values:

${\displaystyle {\begin{aligned}{\frac {22}{7}}&=3.{\overline {142\,857}},\\\pi \,&=3.141\,592\,65\ldots \end{aligned}}}$

The approximation has been known since antiquity. Archimedes wrote the first known proof that ⁠22/7⁠ is an overestimate in the 3rd century BCE, although he may not have been the first to use that approximation. His proof proceeds by showing that ⁠22/7⁠ is greater than the ratio of the perimeter of a regular polygon with 96 sides to the diameter of a circle it circumscribes.

Proof

The proof first devised by British electrical engineer Donald Percy Dalzell (1898–1988) in 1944 can be expressed very succinctly:

${\displaystyle 0<\int _{0}^{1}{\frac {x^{4}\left(1-x\right)^{4}}{1 x^{2}}}\,dx={\frac {22}{7}}-\pi .}$

Therefore, ⁠22/7⁠ > π.

The evaluation of this integral was the first problem in the 1968 Putnam Competition. It is easier than most Putnam Competition problems, but the competition often features seemingly obscure problems that turn out to refer to something very familiar. This integral has also been used in the entrance examinations for the Indian Institutes of Technology.

Details of evaluation of the integral

That the integral is positive follows from the fact that the integrand is non-negative; the denominator is positive and the numerator is a product of nonnegative numbers. One can also easily check that the integrand is strictly positive for at least one point in the range of integration, say at ⁠1/2⁠. Since the integrand is continuous at that point and nonnegative elsewhere, the integral from 0 to 1 must be strictly positive.

It remains to show that the integral in fact evaluates to the desired quantity:

${\displaystyle {\begin{aligned}0&<\int _{0}^{1}{\frac {x^{4}\left(1-x\right)^{4}}{1 x^{2}}}\,dx\\[8pt]&=\int _{0}^{1}{\frac {x^{4}-4x^{5} 6x^{6}-4x^{7} x^{8}}{1 x^{2}}}\,dx&{\text{expansion of terms in the numerator}}\\[8pt]&=\int _{0}^{1}\left(x^{6}-4x^{5} 5x^{4}-4x^{2} 4-{\frac {4}{1 x^{2}}}\right)\,dx&{\text{ using polynomial long division}}&\\[8pt]&=\left.\left({\frac {x^{7}}{7}}-{\frac {2x^{6}}{3}} x^{5}-{\frac {4x^{3}}{3}} 4x-4\arctan {x}\right)\,\right|_{0}^{1}&{\text{definite integration}}\\[6pt]&={\frac {1}{7}}-{\frac {2}{3}} 1-{\frac {4}{3}} 4-\pi \quad &{\text{with }}\arctan(1)={\frac {\pi }{4}}{\text{ and }}\arctan(0)=0\\[8pt]&={\frac {22}{7}}-\pi .&{\text{addition}}\end{aligned}}}$

(See polynomial long division.)

Quick upper and lower bounds

In Dalzell (1944), it is pointed out that if 1 is substituted for x in the denominator, one gets a lower bound on the integral, and if 0 is substituted for x in the denominator, one gets an upper bound:

${\displaystyle {\frac {1}{1260}}=\int _{0}^{1}{\frac {x^{4}\left(1-x\right)^{4}}{2}}\,dx<\int _{0}^{1}{\frac {x^{4}\left(1-x\right)^{4}}{1 x^{2}}}\,dx<\int _{0}^{1}{\frac {x^{4}\left(1-x\right)^{4}}{1}}\,dx={1 \over 630}.}$

Thus we have

${\displaystyle {\frac {22}{7}}-{\frac {1}{630}}<\pi <{\frac {22}{7}}-{\frac {1}{1260}},}$

hence 3.1412 < π < 3.1421 in decimal expansion. The bounds deviate by less than 0.015% from π. See also Dalzell (1971).

Proof that 355/113 exceeds π

As discussed in Lucas (2005), the well-known Diophantine approximation and far better upper estimate ⁠355/113⁠ for π follows from the relation

${\displaystyle 0<\int _{0}^{1}{\frac {x^{8}\left(1-x\right)^{8}\left(25 816x^{2}\right)}{3164\left(1 x^{2}\right)}}\,dx={\frac {355}{113}}-\pi .}$

${\displaystyle {\frac {355}{113}}=3.141\,592\,92\ldots ,}$

where the first six digits after the decimal point agree with those of π. Substituting 1 for x in the denominator, we get the lower bound

${\displaystyle \int _{0}^{1}{\frac {x^{8}\left(1-x\right)^{8}\left(25 816x^{2}\right)}{6328}}\,dx={\frac {911}{5\,261\,111\,856}}=0.000\,000\,173\ldots ,}$

substituting 0 for x in the denominator, we get twice this value as an upper bound, hence

${\displaystyle {\frac {355}{113}}-{\frac {911}{2\,630\,555\,928}}<\pi <{\frac {355}{113}}-{\frac {911}{5\,261\,111\,856}}\,.}$

In decimal expansion, this means 3.141 592 57 < π < 3.141 592 74, where the bold digits of the lower and upper bound are those of π.

Extensions

The above ideas can be generalized to get better approximations of π; see also Backhouse (1995) and Lucas (2005) (in both references, however, no calculations are given). For explicit calculations, consider, for every integer n ≥ 1,

${\displaystyle {\frac {1}{2^{2n-1}}}\int _{0}^{1}x^{4n}(1-x)^{4n}\,dx<{\frac {1}{2^{2n-2}}}\int _{0}^{1}{\frac {x^{4n}(1-x)^{4n}}{1 x^{2}}}\,dx<{\frac {1}{2^{2n-2}}}\int _{0}^{1}x^{4n}(1-x)^{4n}\,dx,}$

where the middle integral evaluates to

${\displaystyle {\begin{aligned}{\frac {1}{2^{2n-2}}}&\int _{0}^{1}{\frac {x^{4n}(1-x)^{4n}}{1 x^{2}}}\,dx\\[6pt]={}&\sum _{j=0}^{2n-1}{\frac {(-1)^{j}}{2^{2n-j-2}(8n-j-1){\binom {8n-j-2}{4n j}}}} (-1)^{n}\left(\pi -4\sum _{j=0}^{3n-1}{\frac {(-1)^{j}}{2j 1}}\right)\end{aligned}}}$

involving π. The last sum also appears in Leibniz' formula for π. The correction term and error bound is given by

${\displaystyle {\begin{aligned}{\frac {1}{2^{2n-1}}}\int _{0}^{1}x^{4n}(1-x)^{4n}\,dx&={\frac {1}{2^{2n-1}(8n 1){\binom {8n}{4n}}}}\\[6pt]&\sim {\frac {\sqrt {\pi n}}{2^{10n-2}(8n 1)}},\end{aligned}}}$

where the approximation (the tilde means that the quotient of both sides tends to one for large n) of the central binomial coefficient follows from Stirling's formula and shows the fast convergence of the integrals to π.

Calculation of these integrals: For all integers k ≥ 0 and ℓ ≥ 2 we have

${\displaystyle {\begin{aligned}x^{k}(1-x)^{\ell }&=(1-2x x^{2})x^{k}(1-x)^{\ell -2}\\[6pt]&=(1 x^{2})\,x^{k}(1-x)^{\ell -2}-2x^{k 1}(1-x)^{\ell -2}.\end{aligned}}}$

Applying this formula recursively 2n times yields

${\displaystyle x^{4n}(1-x)^{4n}=\left(1 x^{2}\right)\sum _{j=0}^{2n-1}(-2)^{j}x^{4n j}(1-x)^{4n-2(j 1)} (-2)^{2n}x^{6n}.}$

Furthermore,

${\displaystyle {\begin{aligned}x^{6n}-(-1)^{3n}&=\sum _{j=1}^{3n}(-1)^{3n-j}x^{2j}-\sum _{j=0}^{3n-1}(-1)^{3n-j}x^{2j}\\[6pt]&=\sum _{j=0}^{3n-1}\left((-1)^{3n-(j 1)}x^{2(j 1)}-(-1)^{3n-j}x^{2j}\right)\\[6pt]&=-(1 x^{2})\sum _{j=0}^{3n-1}(-1)^{3n-j}x^{2j},\end{aligned}}}$

where the first equality holds, because the terms for 1 ≤ j ≤ 3n – 1 cancel, and the second equality arises from the index shift j → j 1 in the first sum.

Application of these two results gives

${\displaystyle {\begin{aligned}{\frac {x^{4n}(1-x)^{4n}}{2^{2n-2}(1 x^{2})}}=\sum _{j=0}^{2n-1}&{\frac {(-1)^{j}}{2^{2n-j-2}}}x^{4n j}(1-x)^{4n-2j-2}\\[6pt]&{}-4\sum _{j=0}^{3n-1}(-1)^{3n-j}x^{2j} (-1)^{3n}{\frac {4}{1 x^{2}}}.\qquad (1)\end{aligned}}}$

For integers k, ℓ ≥ 0, using integration by parts ℓ times, we obtain

${\displaystyle {\begin{aligned}\int _{0}^{1}x^{k}(1-x)^{\ell }\,dx&={\frac {\ell }{k 1}}\int _{0}^{1}x^{k 1}(1-x)^{\ell -1}\,dx\\[6pt]&\,\,\,\vdots \\[6pt]&={\frac {\ell }{k 1}}{\frac {\ell -1}{k 2}}\cdots {\frac {1}{k \ell }}\int _{0}^{1}x^{k \ell }\,dx\\[6pt]&={\frac {1}{(k \ell 1){\binom {k \ell }{k}}}}.\qquad (2)\end{aligned}}}$

Setting k = ℓ = 4n, we obtain

${\displaystyle \int _{0}^{1}x^{4n}(1-x)^{4n}\,dx={\frac {1}{(8n 1){\binom {8n}{4n}}}}.}$

Integrating equation (1) from 0 to 1 using equation (2) and arctan(1) = ⁠π/4⁠, we get the claimed equation involving π.

The results for n = 1 are given above. For n = 2 we get

${\displaystyle {\frac {1}{4}}\int _{0}^{1}{\frac {x^{8}(1-x)^{8}}{1 x^{2}}}\,dx=\pi -{\frac {47\,171}{15\,015}}}$

and

${\displaystyle {\frac {1}{8}}\int _{0}^{1}x^{8}(1-x)^{8}\,dx={\frac {1}{1\,750\,320}},}$

hence 3.141 592 31 < π < 3.141 592 89, where the bold digits of the lower and upper bound are those of π. Similarly for n = 3,

${\displaystyle {\frac {1}{16}}\int _{0}^{1}{\frac {x^{12}\left(1-x\right)^{12}}{1 x^{2}}}\,dx={\frac {431\,302\,721}{137\,287\,920}}-\pi }$

with correction term and error bound

${\displaystyle {\frac {1}{32}}\int _{0}^{1}x^{12}(1-x)^{12}\,dx={\frac {1}{2\,163\,324\,800}},}$

hence 3.141 592 653 40 < π < 3.141 592 653 87. The next step for n = 4 is

${\displaystyle {\frac {1}{64}}\int _{0}^{1}{\frac {x^{16}(1-x)^{16}}{1 x^{2}}}\,dx=\pi -{\frac {741\,269\,838\,109}{235\,953\,517\,800}}}$

with

${\displaystyle {\frac {1}{128}}\int _{0}^{1}x^{16}(1-x)^{16}\,dx={\frac {1}{2\,538\,963\,567\,360}},}$

which gives 3.141 592 653 589 55 < π < 3.141 592 653 589 96.

See also

• Approximations of π
• Chronology of computation of π
• Lindemann–Weierstrass theorem (proof that π is transcendental)
• List of topics related to π
• Proof that π is irrational

Footnotes

Notes

Citations

External links

• The problems of the 1968 Putnam competition, with this proof listed as question A1.